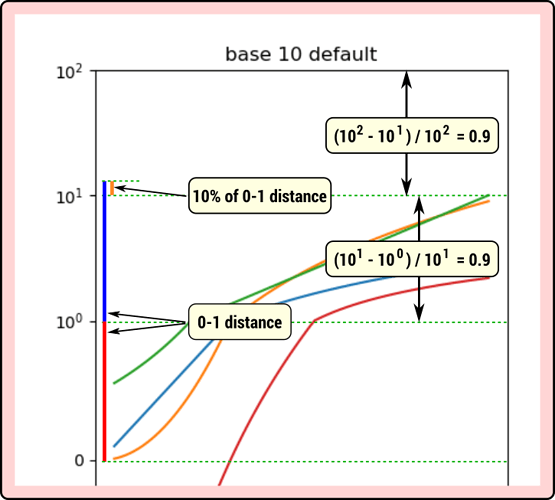
In relation to this discussion on gitter:
I’ve had a look at this and observed something mathematically rather intriguing. For base 10, distances to subsequent decade tick marks all seem to be 90% of the 0-1 decade distance. There is a clear mathematical relationship at work here, as shown in the diagram below, which uses the code from issue number #10369 to generate the graph which I’ve annotated manually in Inkscape.
Is this an intentional part of the scaling design or should tick marks be equally spaced for all decades?
I believe its intentional so that the derivative of a line remains smooth, but the docs do not state that intention, and it causes substantial confusion, particularly if you look at the code, and realize it could not possibly be doing what the docs say.
I think the people who use this scale are fine with this behaviour, and were likely not counting on the ticks being exactly equally spaced, but I think the behaviour should be documented. However, I still think its pretty bad to not have an explicit inverse that you can readily describe in a paper; I’ve definitely digitized by hand results from old papers, and if they had used this scale, I’d be off based on the description in the docstring and captions of the figures, and actually substantially off in absolute number space.
Ah. I see. Curious to understand how it guarantees smooth derivative (just thinking out loud to myself, as a former - if slightly rusty - mathematician).
If the behaviour is to remain as is but be better documented, perhaps the mathematical relation I identified above may help to explain the ratio between first b-ade width/height and subsequent ones. It works for all bases.
I should perhaps be a little clearer here and state that the ratio of lengths between the logarithmic b-ades and the linear b-ade is governed by the following mathematical relation
(base - 1) / base
e.g.
base 10: (10 - 1) / 10 = 0.9
base e: (2.71828 - 1) / 2.71828 = 0.632
base 2: (2 - 1) / 2 = 0.5
So, in base 2, the linear b-ade is exactly twice the length of the logarithmic b-ade.
TBH… the fact that the magnitude of this effect varies by base and is so much more apparent at lower base values does seem to be a little disconcerting to me as a mathematician. However, as I have no specific use case here my views are theoretical only.