Hi all,
I would like to use griddata() to interpolate a function given at specified points of a bunch of other points. While the method works well, it slows down considerably as the number of points to interpolate to increases.
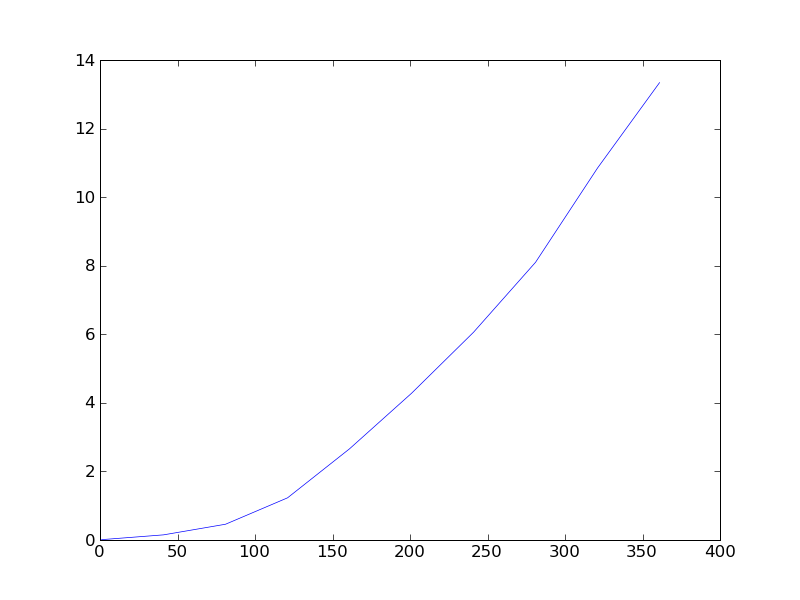
The dependence of time/(number of points) is nonlinear (see the attachment) - it seems that while the Delaunay trinagulation itself is fast, I wonder how to speed-up the interpolation. The docstring says, that it is based on "natural neighbor interpolation" - how are the neighbors searched? Does it use the kd-trees like scipy.spatial? I have a very good experience with scipy.spatial performance.
Also, is there a way of reusing the triangulation when interpolating several times using the same grid?
cheers,
r.
ps: no natgrid
In [9]: mpl.__version__
Out[9]: '0.98.5.3'