Scatter Plot Animation

Community
1

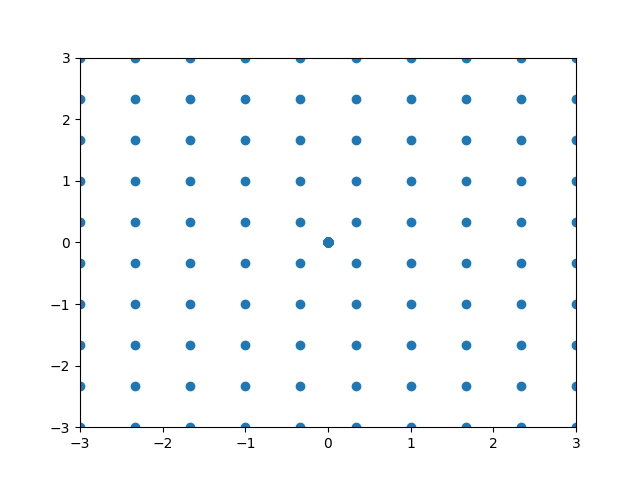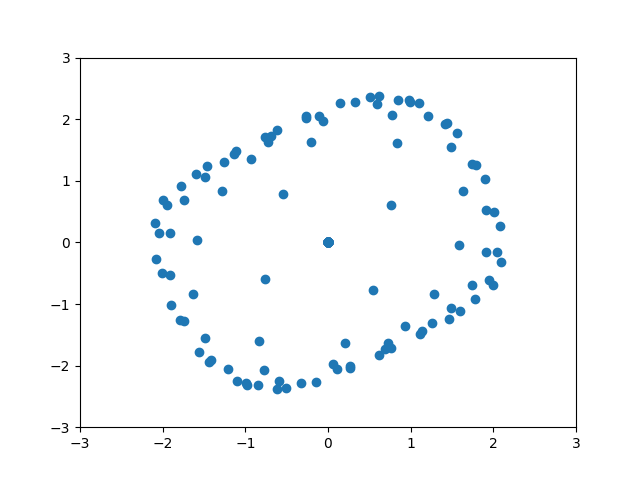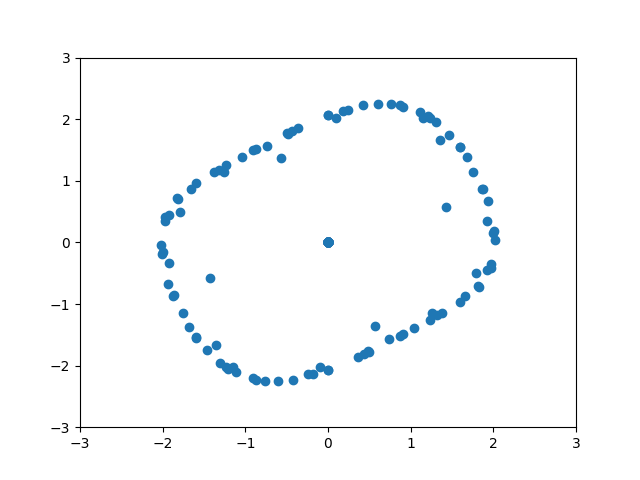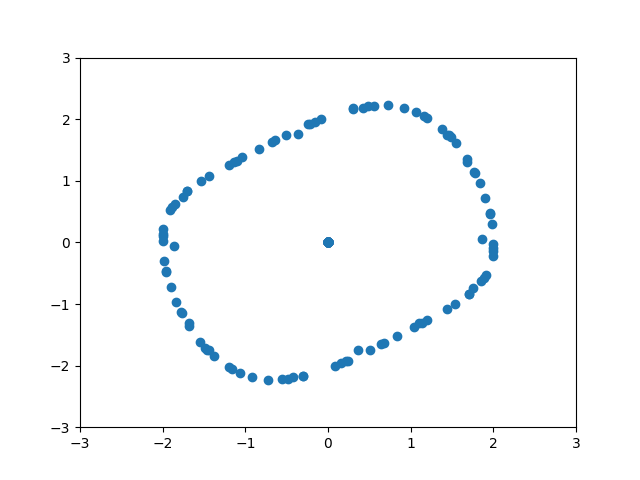
Hey, I’ve been at this for a couple hours so hopefully y’all have better luck. I am trying to animate a data set. I know the computations and data set are right because when I plot each frame individually I get the desired result. When I try to animate, however, I get a mess (so I think it has to be in how I’m animating it). The output should look like fluid rotating. Any help would be greatly appreciated!

Code:

import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
from matplotlib.animation import FuncAnimation
from functools import partial

#system
def van_der_pol(coords, t, mu, evens, odds, ones):
    x, y = coords*evens, coords*odds
    x_shift = np.roll(x, 1) #for use in computation
    y_prime = mu*(1-x_shift**2)*y-x_shift
    return np.roll(y, -1)+y_prime

#initialize window for blitting
def init(fig, axes, scatter):
    plt.xlim([-3.0, 3.0])
    plt.ylim([-3.0, 3.0])
    return scatter,

#animates one frame
def animate(t, sols, scatter, odds, evens):
    print(t)

    scatter.set_offsets(np.array([np.trim_zeros(sols[t]*evens), np.trim_zeros(sols[t]*odds)]))
    return scatter,
    
#constants
mu = 0.5

#initial data
M = 10
axis = np.linspace(-3.0, 3.0, M)
init_conds = np.array([(x, y) for x in axis for y in axis])
init_conds = init_conds.reshape(2*M**2)
evens, odds = np.array([1 if i % 2 == 0 else 0 for i in range(2*M**2)]), np.array([1 if i % 2 == 1 else 0 for i in range(2*M**2)]) #will be used to extract the x and y coordinates
ones = np.ones(2*M**2)

#solving
total = 10.0
delta = 0.1
N = int(total/delta)
t = np.linspace(0.0, total, N)
sols = odeint(van_der_pol, init_conds, t, args=(mu, evens, odds, ones))

#setup
fig, axes = plt.figure(), plt.axes(frameon=True)
scatter = plt.scatter([], [], animated=True)

#animation
anim = FuncAnimation(fig, func=animate, frames=N, init_func=partial(init, fig, axes, scatter), blit=True, fargs=(sols, scatter, odds, evens), repeat=False)
anim.save("out.mp4", fps=40)
plt.show()

(edited by @ianhi to put code in post)

2

What version of matplotlib are you using? When I run your code I get the following value error:

ValueError: 'vertices' must be 2D with shape (M, 2). Your input has shape (2, 199).

So I suspect you are using older version of mpl where that error is not raised. The solution to this is to replace the np.array call in the animate function with np.column_stack:

scatter.set_offsets(np.column_stack([np.trim_zeros(sols[t]*evens), np.trim_zeros(sols[t]*odds)]))

which gives me a nice looking rotating
out

1 Like
3

Also you can avoid having to deal with things like set_offsets if you use mpl-interactions which makes it easy to make dynamic plots where you control parameters (in this case time) using sliders and then to save animations of them. In your case you could drop the animate function and just do the following for making a plot. (I added some nice indexing slicing in order to get the even and odd parts)

# plotting and creating an interactive figure
from mpl_interactions import indexer
from mpl_interactions import ipyplot as iplt
fig, axes = plt.figure(), plt.axes(frameon=True)
ctrls = iplt.scatter(indexer(sols[:, ::2], "T"), indexer(sols[:, 1::2], "T"), T=np.arange(50))


# saving an animation
ctrls.save_animation('out.gif', fig, 'T', interval=75)

There are two examples of interactvieyl solving ODEs using mpl-interactions you may also be interested in:
https://mpl-interactions.readthedocs.io/en/stable/examples/rossler-attractor.html
https://mpl-interactions.readthedocs.io/en/stable/examples/Lotka-Volterra.html

1 Like
4

Thanks! I ended up finding a solution which was pretty similar to your first comment. I will take a look at the indexing stuff. I do a lot of this type of stuff, so that would probably help a great deal.

5

The indexing [:,::2] is just using the stepsize parameter of slice objects. You can see what that’s doing by np.arange(100)[::2]

mpl-interactions works by accepting a function for the X and Y arguments of the functions like scatter, so the indexer is just a convenience wrapper for:

def f(*args, **kwargs):
   # some stuf...
    return arr[idx]

in general however it can be any python function