Possible bug with contour plots

Community
1

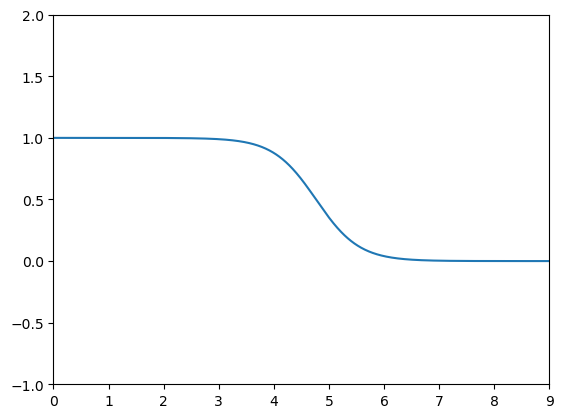
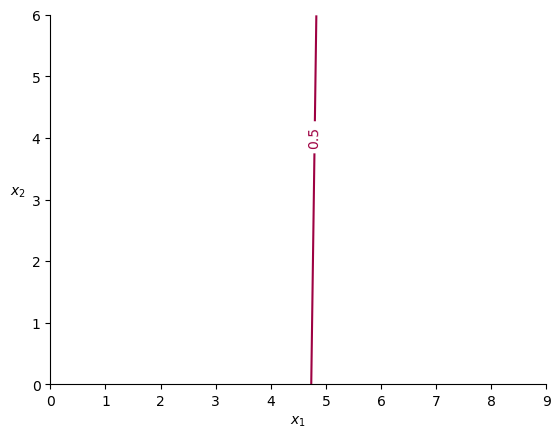
I have a question regarding a contour plot. I got a minimal working example which shows the issue. Let’s walk through that, my question is at the end.

Definition of functions g_1, g_2 and compound function g:

import matplotlib.pyplot as plt
import torch

w_1 = torch.tensor([0.9912, 1.0234])
w_10 = torch.tensor([-3.3894])

w_2 = torch.tensor([3.5639, 0.9837])
w_20 = torch.tensor([-15.5668])

def g_1(x):
    return x.matmul(w_1) + w_10

def g_2(x):
    return x.matmul(w_2) + w_20

def g(x):
    return g_1(x) / g_2(x)

When we plot g(x_1, x_2) at fixed x_2 = 2.0 we get the following plot:

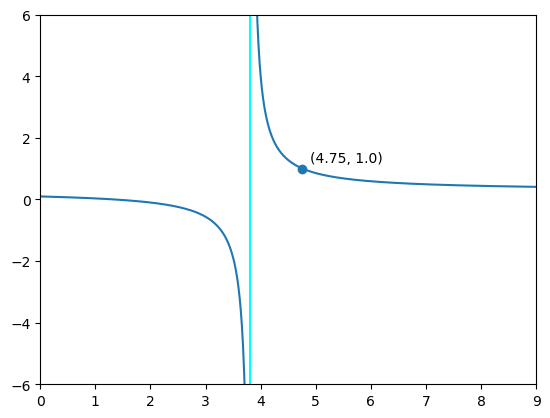
image

There is a discontinuity at around x_1 = 3.8 and g(x_1, 2.0) = 1 at around x_1 = 4.75.

Source of plot:

xmin = 0
xmax = 9
ymin = -6
ymax = 6

x = torch.arange(xmin, xmax, 0.01)
xx = torch.stack([x, torch.full(x.shape, 2.0)], dim=1)

z = g(xx)

fig, ax = plt.subplots()

idx = torch.argmax(torch.diff(torch.sign(z))) + 1
x[idx] = torch.nan
z[idx] = torch.nan

ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)

ax.vlines(x=3.80, ymin=ymin, ymax=ymax, colors='aqua')
ax.scatter(x=4.75, y=1.0)
ax.annotate('(4.75, 1.0)', (4.9, 1.2))

plt.plot(x, z)
plt.show()

Now if we draw a contour plot of g(x) at the single level 1.0 (the case when g_1(x) = g_2(x)), then we get the following plot:

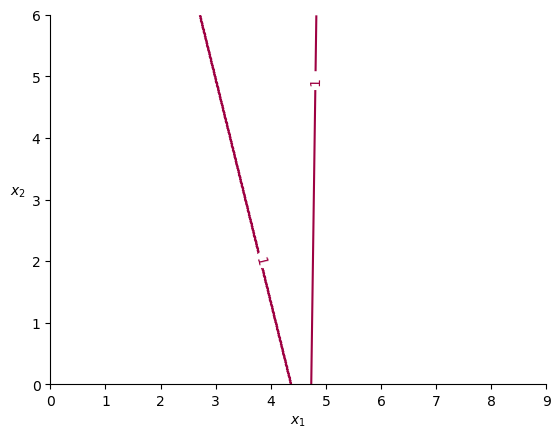
image

The right line represents all x where g(x) = 1

My question: why does the left line appear? It seems not to be a correct contour line, it appears to represent the discontinuity of g(x).

Source of plot:

xmin = 0
xmax = 9
ymin = 0
ymax = 6
h = 0.01

fig, ax = plt.subplots()

X = torch.arange(xmin, xmax, h)
Y = torch.arange(ymin, ymax, h)
XX, YY = torch.meshgrid(X, Y, indexing='xy')

ZZ = torch.stack([XX.ravel(), YY.ravel()], dim=1)
ZZ = g(ZZ)
ZZ = ZZ.reshape(XX.shape)
cs = ax.contour(XX, YY, ZZ, cmap=plt.cm.Spectral, levels=[1.0])
ax.clabel(cs, inline=True, fontsize=10)

ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
ax.set_xlabel('$x_1$')
ax.yaxis.label.set(rotation='horizontal', ha='right')
ax.set_ylabel('$x_2$', labelpad=10)
ax.spines[['right', 'top']].set_visible(False)

plt.show()
2

The contouring algorithm is explained at Algorithm description - ContourPy documentation.

It doesn’t calculate the contours of your continuous analytical function, it calculates the contours of the 2D gridded discretisation of the function that you pass to it and interpolates between the z-values at the grid points. If you have grid points either side of your discontinuity then one will have a large negative z-value and the other a large positive z-value, so the line between them contains all possible z-values between those two extremes. If you ask for a contour line to be calculated at any z-level between those two extremes then this edge will be intersected by such a contour.

What you are expecting is for the contouring algorithm to somehow know that there is an infinite discontinuity along certain edges of your 2D grid. It doesn’t know this.

What could you do about this? You could calculate the contours either side of the discontinuity separately. Alternatively you could mask out that part of the domain that straddles the discontinuity to exclude it. Because the masking is performed on a per-grid point basis (z array, mask and corner mask - ContourPy documentation) you’d have to insert a row/column of dummy points for this. This is easy if the discontinuity is row or column-aligned, more difficult otherwise. Plus it requires you to know in advance where the discontinuity is.

1 Like
3

Thanks for the explanation! :+1:

As a workaround I use now a softmax normalization:

g(x) = \frac{\exp(g_1(x))}{\exp(g_1(x)) + \exp(g_2(x))}

This shows the following curve (at x_2 = 2.0):

image

And this is the contour plot with a single level 0.5:

image