Plotting Scalar on a Circular Grid

Community matplotlib-users
1

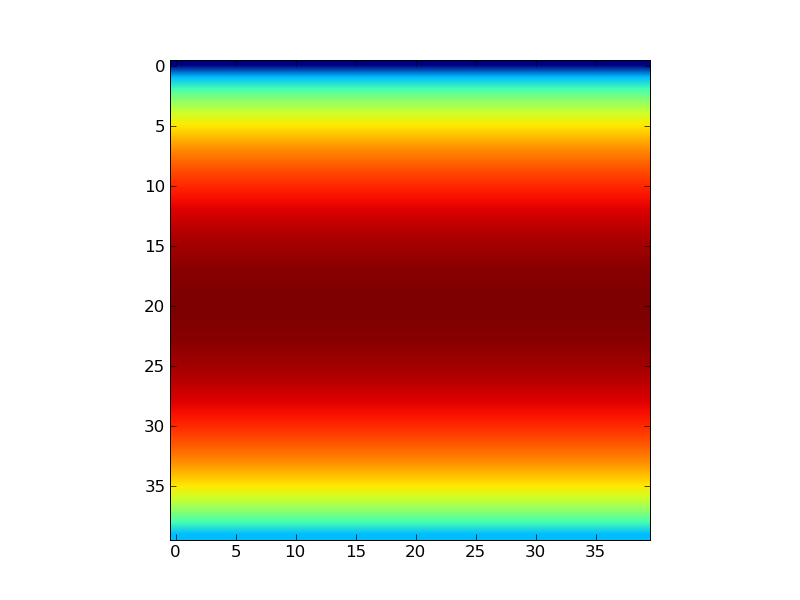
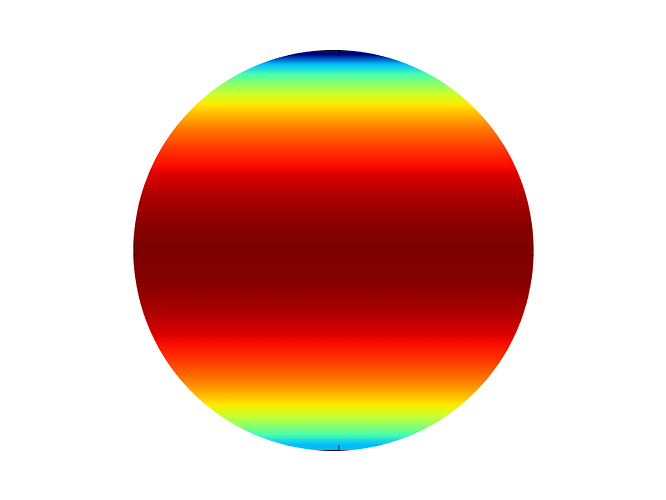
Dear All,
I am having a hard time with something which must be fairly doable: I
would like to plot a simple scalar function on a circular domain.
Consider for instance a trivial modification of one of the online examples:

Code 1

#!/usr/bin/env python
"""
See pcolor_demo2 for a much faster way of generating pcolor plots
"""
from __future__ import division
from pylab import *

def func3(x,y):
    return (1- x/2 + x**5 + y**3)*exp(-x**2-y**2)

def func4(x,y):
    theta=arcsin(y)
    return cos(theta)

# make these smaller to increase the resolution
dx, dy = 0.05, 0.05

x = arange(-1.0, 1.0, dx)
y = arange(-1.0, 1.0, dy)
X,Y = meshgrid(x, y)

Z = func4(X, Y)

print "Z is, ", Z

ax = subplot(111)
im = imshow(Z, cmap=cm.jet)
#im.set_interpolation('nearest')
#im.set_interpolation('bicubic')
im.set_interpolation('bilinear')
#ax.set_image_extent(-3, 3, -3, 3)

show()

Now, I would like to plot exactly the same function but on a circular
domain (circle of radius 1 centered at (0,0)).
What is the easiest way of doing that? Some time ago I came across a
similar problem (again, plotting a scalar on a circular domain) and I
came up with this code (thanks to the help I got from the list)

Code 2

#! /usr/bin/env python
from scipy import *
import pylab
import numpy

nt=20
nr=20

r=linspace(0.,10.,nr)

theta=linspace(0.,2.*pi,nt)
#print "theta is ", theta
sin_t=sin(theta)
cos_t=cos(theta)
rsin_t=r[newaxis,:]*sin_t[:,newaxis]
rcos_t=r[newaxis,:]*cos_t[:,newaxis]
rsin_t=ravel(rsin_t)
rcos_t=ravel(rcos_t)

rsin_t.shape=(nt,nr)
rcos_t.shape=(nt,nr)

vel_section=numpy.random.normal(0.,5.,(nr*nt))

vel_section=reshape(vel_section,(nt,nr))
print 'OK up to here'

#pylab.colorbar()
#pylab.clf()
pylab.figure()
X = rsin_t.transpose()
Y = rcos_t.transpose()
Z = vel_section.transpose()
velmin = vel_section.min()
velmax = vel_section.max()
print velmin, velmax
levels = arange(velmin, velmax+0.01, 0.1)
pylab.contourf(X, Y, Z, levels, cmap=pylab.cm.jet)
pylab.colorbar()

pylab.show()

pylab.savefig("velocity_on_section_DNS")
#pylab.hold(False)

but I have been unable to modify it according to my present needs.
I am not really finding my way through the documentation/examples for
some details (for instance, I am not sure about how to include a
discrete colorbar ranging from 0 to 1 in steps of 0.1 in code 1), but
at the moment this is secondary probably.
Any suggestion is welcome.
Many thanks

Lorenzo

···

--
Life is what happens to you while you're busy making other plans.

2

You have an image with x,y spanning from -1 to 1. How do you transform
your x,y coordinate to r, theta? Or, x,y in your example actually
corresponds to r, theta in polar coordinate?
In that case, is it simply that you want to your image centered at
(0,0)? Use the extent keyword of imshow command.

  http://matplotlib.sourceforge.net/api/pyplot_api.html#matplotlib.pyplot.imshow

It is not clear what you want.
Regards,

-JJ

···

On Wed, Apr 1, 2009 at 6:50 AM, Lorenzo Isella <lorenzo.isella@...287...> wrote:

Now, I would like to plot exactly the same function but on a circular
domain (circle of radius 1 centered at (0,0)).

3

Hello,
I'll try to make myself clear with a simple example: consider a circle
in 2D Cartesian coordinates (x,y) (my domain).
On that circle, for each (x,y) coordinate, you want to plot the function

f(x,y)=x+y

How would you do that in pylab? perhaps I should have called this a
surface plot (as if I was plotting a temperature field on a tube
cross-section)
This is easy to do in pylab if the domain is e.g. a square, but I do
not know how to handle the simple case I described above conveniently.
Many thanks

Lorenzo

2009/4/2 Jae-Joon Lee <lee.j.joon@...287...>:

···

On Wed, Apr 1, 2009 at 6:50 AM, Lorenzo Isella <lorenzo.isella@...287...> wrote:

Now, I would like to plot exactly the same function but on a circular
domain (circle of radius 1 centered at (0,0)).

You have an image with x,y spanning from -1 to 1. How do you transform
your x,y coordinate to r, theta? Or, x,y in your example actually
corresponds to r, theta in polar coordinate?
In that case, is it simply that you want to your image centered at
(0,0)? Use the extent keyword of imshow command.

http://matplotlib.sourceforge.net/api/pyplot_api.html#matplotlib.pyplot.imshow

It is not clear what you want.
Regards,

-JJ

--
Life is what happens to you while you're busy making other plans.

4

I'm afraid that I'm still confused and there seems to be not much
thing I can help..

You're considering a circle, but you already have your function in a
cartesian coordinate. I'm not sure why you can't just plot in a
cartesian coordinate? (in other words, what is wrong with your
original script?)

There is an "set_image_extent" call in your original script (although
commented out). Maybe what you're trying to do is simply

im = imshow(Z, cmap=cm.jet, extent=(-3, 3, -3, 3))

I'm not sure it would be relevant, but if you have your function or
data in (r, theta) coordinate, one simple way is just to use the
polar axes with pcolormesh method.

n_theta, n_r = 100, 50
theta = np.linspace(0, 2*np.pi, n_theta+1)
r = np.linspace(0., 1., n_r + 1)
data = np.arange(0., n_theta*n_r).reshape(n_r, n_theta)
ax=subplot(1,1,1, projection="polar", aspect=1.)
ax.pcolormesh(theta, r, data)

-JJ

5

Hello,
So maybe a couple of images can help.
Using the code

#!/usr/bin/env python
"""
See pcolor_demo2 for a much faster way of generating pcolor plots
"""
from __future__ import division
from pylab import *

def func3(x,y):
   return (1- x/2 + x**5 + y**3)*exp(-x**2-y**2)

def func4(x,y):
   theta=arcsin(y)
   return cos(theta)

# make these smaller to increase the resolution
dx, dy = 0.05, 0.05

x = arange(-1.0, 1.0, dx)
y = arange(-1.0, 1.0, dy)
X,Y = meshgrid(x, y)

Z = func4(X, Y)

print "Z is, ", Z

ax = subplot(111)
im = imshow(Z, cmap=cm.jet)
#im.set_interpolation('nearest')
#im.set_interpolation('bicubic')
im.set_interpolation('bilinear')
#ax.set_image_extent(-3, 3, -3, 3)

show()

I can get the attached image.png, but what I am really after is
image2.png (the same quantity plotted on a circular domain!). How can
I achieve that (without using scissors on an existing image?).
This is what I meant from start.
Cheers

Lorenzo

2009/4/3 Jae-Joon Lee <lee.j.joon@...287...>:

image.png
image.png800×600 9.09 KB

image2.png
image2.png800×600 10 KB

···

I'm afraid that I'm still confused and there seems to be not much
thing I can help..

You're considering a circle, but you already have your function in a
cartesian coordinate. I'm not sure why you can't just plot in a
cartesian coordinate? (in other words, what is wrong with your
original script?)

There is an "set_image_extent" call in your original script (although
commented out). Maybe what you're trying to do is simply

im = imshow(Z, cmap=cm.jet, extent=(-3, 3, -3, 3))

I'm not sure it would be relevant, but if you have your function or
data in (r, theta) coordinate, one simple way is just to use the
polar axes with pcolormesh method.

n_theta, n_r = 100, 50
theta = np.linspace(0, 2*np.pi, n_theta+1)
r = np.linspace(0., 1., n_r + 1)
data = np.arange(0., n_theta*n_r).reshape(n_r, n_theta)
ax=subplot(1,1,1, projection="polar", aspect=1.)
ax.pcolormesh(theta, r, data)

-JJ

--
Life is what happens to you while you're busy making other plans.

6

There are a few ways to do that depending on exactly what you want.

From your script, you may just clip your image.

im = imshow(Z, extent=(-1, 1, -1, 1))
im.set_clip_path(Circle((0,0),1, transform=ax.transData))

(Note the use of extent keyword in imshow)

Or,

You can use polar coordinate with pcolormesh for image display. But
your data need to be defined in the polar coordinate, unlike your
script.

# function defined in polar coordinate
def func5(theta, r):
    y = r*np.sin(theta)
    theta=np.arcsin(y)
    return np.cos(theta)

R=1.
n_theta, n_r = 360, 100

# cooridnates of the mesh
theta = np.linspace(0, 2*np.pi, n_theta+1)
r = np.linspace(0., R, n_r + 1)

dr, dtheta = r[1]-r[0], theta[1]-theta[0]

# cooridnate for the data point
theta_d = np.arange(dtheta/2., 2*np.pi, dtheta)
r_d = np.arange(dr/2., R, dr)

TT, RR = meshgrid(theta_d, r_d)
Z = func5(TT, RR)

ax=subplot(1,1,1, projection="polar", aspect=1.)
ax.pcolormesh(theta, r, Z)

-JJ

···

On Mon, Apr 6, 2009 at 6:35 AM, Lorenzo Isella <lorenzo.isella@...287...> wrote:

Hello,
So maybe a couple of images can help.
Using the code

#!/usr/bin/env python
"""
See pcolor_demo2 for a much faster way of generating pcolor plots
"""
from __future__ import division
from pylab import *

def func3(x,y):
return (1- x/2 + x**5 + y**3)*exp(-x**2-y**2)

def func4(x,y):
theta=arcsin(y)
return cos(theta)

# make these smaller to increase the resolution
dx, dy = 0.05, 0.05

x = arange(-1.0, 1.0, dx)
y = arange(-1.0, 1.0, dy)
X,Y = meshgrid(x, y)

Z = func4(X, Y)

print "Z is, ", Z

ax = subplot(111)
im = imshow(Z, cmap=cm.jet)
#im.set_interpolation('nearest')
#im.set_interpolation('bicubic')
im.set_interpolation('bilinear')
#ax.set_image_extent(-3, 3, -3, 3)

show()

I can get the attached image.png, but what I am really after is
image2.png (the same quantity plotted on a circular domain!). How can
I achieve that (without using scissors on an existing image?).
This is what I meant from start.
Cheers

Lorenzo

2009/4/3 Jae-Joon Lee <lee.j.joon@...287...>:

I'm afraid that I'm still confused and there seems to be not much
thing I can help..

You're considering a circle, but you already have your function in a
cartesian coordinate. I'm not sure why you can't just plot in a
cartesian coordinate? (in other words, what is wrong with your
original script?)

There is an "set_image_extent" call in your original script (although
commented out). Maybe what you're trying to do is simply

im = imshow(Z, cmap=cm.jet, extent=(-3, 3, -3, 3))

I'm not sure it would be relevant, but if you have your function or
data in (r, theta) coordinate, one simple way is just to use the
polar axes with pcolormesh method.

n_theta, n_r = 100, 50
theta = np.linspace(0, 2*np.pi, n_theta+1)
r = np.linspace(0., 1., n_r + 1)
data = np.arange(0., n_theta*n_r).reshape(n_r, n_theta)
ax=subplot(1,1,1, projection="polar", aspect=1.)
ax.pcolormesh(theta, r, data)

-JJ

--
Life is what happens to you while you're busy making other plans.