plot a triangular mesh

Community matplotlib-users
1

Hi,

I have a set of vertices in 2D as triples (x, y, val), where the x, y
are 2D coordinates and "val" is the scalar value of the finite element
solution, here is an example:

In [54]: l.get_vertices()
Out[54]:
array([[ 0.00000000e+00, -1.00000000e+00, -2.22396971e-17],
       [ 1.00000000e+00, -1.00000000e+00, -1.64798730e-17],
       [ -1.00000000e+00, 0.00000000e+00, 8.09899023e-17],
       ...,
       [ 1.48437500e-01, -1.56250000e-02, 1.62359362e-01],
       [ 1.32812500e-01, 0.00000000e+00, 1.56012622e-01],
       [ 1.32812500e-01, -1.56250000e-02, 1.50562411e-01]])

and I also have a set of triangles that connect those points, here is
an example:

In [55]: l.get_triangles()
Out[55]:
array([[ 3, 5448, 29],
       [ 27, 5445, 28],
       [ 29, 28, 26],
       ...,
       [5499, 5498, 5479],
       [5510, 5493, 5491],
       [5513, 5508, 5491]], dtype=int32)

The triangles define the 2D domain. What is the best way to get this
plotted with mpl? Should I write a loop using the "plot" command, or
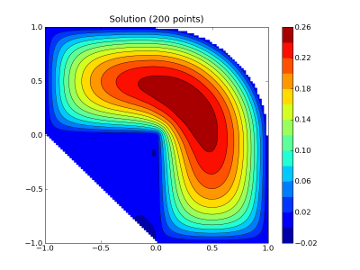
is there a better alternative? So far, I am using the contour command
and I feed it just with the vertices, here is the code:

    vert = lin.get_vertices()
    from numpy import min, max, linspace
    from matplotlib.mlab import griddata
    import matplotlib.pyplot as plt
    # make up data.
    #npts = int(raw_input('enter # of random points to plot:'))
    npts = 200
    x = vert[:, 0]
    y = vert[:, 1]
    z = vert[:, 2]
    # define grid.
    xi = linspace(min(x), max(x), 100)
    yi = linspace(min(y), max(y), 100)
    # grid the data.
    zi = griddata(x,y,z,xi,yi)
    # contour the gridded data, plotting dots at the nonuniform data points.
    CS = plt.contour(xi,yi,zi,15,linewidths=0.5,colors='k')
    CS = plt.contourf(xi,yi,zi,15,cmap=plt.cm.jet)
    plt.colorbar() # draw colorbar
    plt.title('Solution (%d points)' % npts)

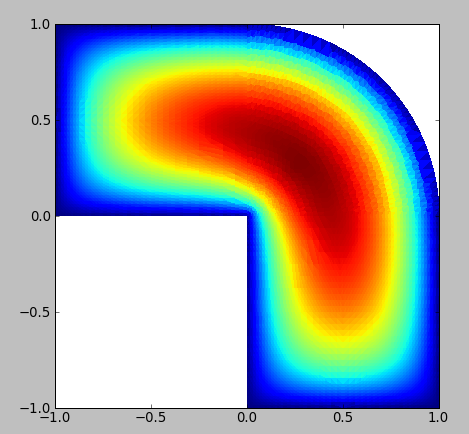
The output of which is attached. It looks ugly, because mpl doesn't
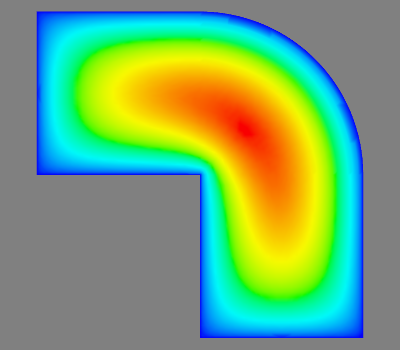
have enough information about the domain. Mayavi can use this
information with this script:

    vert = lin.get_vertices()
    triangles = lin.get_triangles()
    from numpy import zeros
    from enthought.mayavi import mlab
    x = vert[:, 0]
    y = vert[:, 1]
    z = zeros(len(y))
    t = vert[:, 2]
    # the off screen rendering properly works only with VTK-5.2 or above:
    mlab.options.offscreen = True
    s = mlab.triangular_mesh(x, y, z, triangles, scalars=t)
    mlab.view(azimuth=90, elevation=180)

the output of which is attached. Mayavi is good, but it's a little
overkill for this purpose, as it takes a while to start etc. I want to
use it inside the Sage notebook, where matplotlib is faster and takes
less memory. Also it's way easier to install (e.g. no vtk, and
fiddling with os mesa).

Thanks for any ideas.

Ondrej

mpl1.png

mayavi.png

2

The best way is to define your triangles as an n length list of
triangle vertices

  verts = [ ( (x00, y00), (x01, y01), (x02, y02)),
                 (x10, y10), (x11, y11), (x12, y12)),
                 ...
    ]

and have an equal length array of intensities for color mapping.

  vals = np.array(N_color_intensities)

Then create a PolyCollection:

  import matplotlib.cm as cm
  import matplotlib.collections as collections
  col = collections.PolyCollection(verts)
  col.set_array(val)
  col.set_cmap(cm.hot)
  ax.add_collection(col)

add_collection doesn't get the autoscaling limits, if I recall
correctly, so you will probably want to do

  ax.set_xlim(xmin, xmax)
  ax.set_ylim(ymin,. ymax)

See also:

  http://matplotlib.sourceforge.net/api/collections_api.html#matplotlib.collections.PolyCollection
  Search — Matplotlib 3.8.2 documentation

Unfortunately, we do not currently have support for interpolating
between adjacent polys in a PolyCollection, so the result may not look
as nice as mayavis.

JDH

···

On Thu, May 21, 2009 at 9:31 PM, Ondrej Certik <ondrej@...2033...> wrote:

Hi,

I have a set of vertices in 2D as triples (x, y, val), where the x, y
are 2D coordinates and "val" is the scalar value of the finite element
solution, here is an example:

In [54]: l.get_vertices()
Out[54]:
array([[ 0.00000000e+00, -1.00000000e+00, -2.22396971e-17],
      [ 1.00000000e+00, -1.00000000e+00, -1.64798730e-17],
      [ -1.00000000e+00, 0.00000000e+00, 8.09899023e-17],
      ...,
      [ 1.48437500e-01, -1.56250000e-02, 1.62359362e-01],
      [ 1.32812500e-01, 0.00000000e+00, 1.56012622e-01],
      [ 1.32812500e-01, -1.56250000e-02, 1.50562411e-01]])

and I also have a set of triangles that connect those points, here is
an example:

In [55]: l.get_triangles()
Out[55]:
array([[ 3, 5448, 29],
      [ 27, 5445, 28],
      [ 29, 28, 26],
      ...,
      [5499, 5498, 5479],
      [5510, 5493, 5491],
      [5513, 5508, 5491]], dtype=int32)

The triangles define the 2D domain. What is the best way to get this
plotted with mpl? Should I write a loop using the "plot" command, or
is there a better alternative? So far, I am using the contour command
and I feed it just with the vertices, here is the code:

3

Here is an example using matplotlib.delaunay, which automatically returns the edges and triangules:

import matplotlib.delaunay as delaunay
import matplotlib.pyplot as pp

#generate points
npts=41
xpt=sp.random.random_sample(npts)
ypt=sp.random.random_sample(npts)
#create triangulation
circumcenters,edges,tri_points,tri_neighbors=delaunay.delaunay(xpt, ypt)
#plot using edges
pp.plot(xpt[edges.T],ypt[edges.T],'b-')

#following extracts same edges from triangles
# but does not worry about repeating edges
from numpy import vstack
my_edges=vstack( (tri_points[:,0:2],
                  tri_points[:,1:],
                  tri_points[:,2::-2]) )
#plot the edges extracted (possibly multiple times) from triangles
pp.plot(xpt[my_edges.T],ypt[my_edges.T],'r--')

4

Hi,

I have a set of vertices in 2D as triples (x, y, val), where the x, y
are 2D coordinates and "val" is the scalar value of the finite element
solution, here is an example:

In [54]: l.get_vertices()
Out[54]:
array([[ 0.00000000e+00, -1.00000000e+00, -2.22396971e-17],
[ 1.00000000e+00, -1.00000000e+00, -1.64798730e-17],
[ -1.00000000e+00, 0.00000000e+00, 8.09899023e-17],
...,
[ 1.48437500e-01, -1.56250000e-02, 1.62359362e-01],
[ 1.32812500e-01, 0.00000000e+00, 1.56012622e-01],
[ 1.32812500e-01, -1.56250000e-02, 1.50562411e-01]])

and I also have a set of triangles that connect those points, here is
an example:

In [55]: l.get_triangles()
Out[55]:
array([[ 3, 5448, 29],
[ 27, 5445, 28],
[ 29, 28, 26],
...,
[5499, 5498, 5479],
[5510, 5493, 5491],
[5513, 5508, 5491]], dtype=int32)

The triangles define the 2D domain. What is the best way to get this
plotted with mpl? Should I write a loop using the "plot" command, or
is there a better alternative? So far, I am using the contour command
and I feed it just with the vertices, here is the code:

The best way is to define your triangles as an n length list of
triangle vertices

verts = [ ( (x00, y00), (x01, y01), (x02, y02)),
(x10, y10), (x11, y11), (x12, y12)),
...
]

and have an equal length array of intensities for color mapping.

vals = np.array(N_color_intensities)

Then create a PolyCollection:

import matplotlib.cm as cm
import matplotlib.collections as collections
col = collections.PolyCollection(verts)
col.set_array(val)
col.set_cmap(cm.hot)
ax.add_collection(col)

add_collection doesn't get the autoscaling limits, if I recall
correctly, so you will probably want to do

ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin,. ymax)

See also:

http://matplotlib.sourceforge.net/api/collections_api.html#matplotlib.collections.PolyCollection
Search — Matplotlib 3.8.2 documentation

Unfortunately, we do not currently have support for interpolating
between adjacent polys in a PolyCollection, so the result may not look
as nice as mayavis.

Thanks a lot John. I tried that and it does what I want. I just need
to convert and probably average my 3 different values at the 3
vertices of the triangle and color the triangle with that color. When
I get it working, I'll send you a picture. :slight_smile:

···

On Fri, May 22, 2009 at 7:06 AM, John Hunter <jdh2358@...287...> wrote:

On Thu, May 21, 2009 at 9:31 PM, Ondrej Certik <ondrej@...2033...> wrote:

On Fri, May 22, 2009 at 7:32 AM, Eric Carlson <ecarlson@...2618...> wrote:

Here is an example using matplotlib.delaunay, which automatically
returns the edges and triangules:

Thanks, that works too -- but it only plots the edges, right? I will
use that to plot the mesh, I need that as well.

For the FE solution, I'll use John's approach.

Ondrej

5

Ok, I made a progress, it seems it's working. Script and picture
attached. You can compare to the mayavi plot above, it's almost
identical now. It took my some time playing with different parameters
of mpl to get here and I think it looks quite good. Still one can see
the artefacts though as John predicted, due to mpl not interpolating
the triangles.

Maybe I should use some graphics library directly, like Cairo, or
something similar? The mpl is also quite slow, I know that if I use
opengl directly, the plot is instant, so there must be some way
(unless the opengl is using the hardware to plot the triangles, which
it may well be).

Ondrej

mpl2.png

···

On Fri, May 22, 2009 at 3:37 PM, Ondrej Certik <ondrej@...2033...> wrote:

Thanks a lot John. I tried that and it does what I want. I just need
to convert and probably average my 3 different values at the 3
vertices of the triangle and color the triangle with that color. When
I get it working, I'll send you a picture. :slight_smile:

6

Ok, I made a progress, it seems it's working. Script and picture

Forgot to attach the script.

Ondrej

t.py (1.48 KB)

7

I should read entire posts before sending people down the wrong pathways. I just happened to be working on a Python equivalent to MATLAB "triplot" stuff when I read your subject line and made the wrong assumptions. That program does just plot the edges, as you noted.

I have attached a python program, much of which is a translation of a program I found at M*B central, contributed from the outside. Given a triangulation, it allows you to interpolate on a regular rectangular grid (dx=constant, dy=another constant). In your case, it should allow you to use your original triangulation, and should avoid the convex hull artifacts of your original griddata plot. I do not know if this new program will give you a figure that will look as good as your latest based on John's suggestion or not.

Just a few warnings:
1. I use an environment that (like matlab but very unpythonic) imports everything, so the attached may need to import one or two more routines

2. I have only tested with generated data, using triangulations created with delaunay, but it worked okay as long as my random points did not lead to bad triangles.

3. The routines use a lot of loops, so they are relatively slow - should be an ideal program for Cython though.

3. method='linear' uses linear interp,and is very stable. It should not be influenced in any way by convexity.

   method='quadratic' uses a quadratic method, which does well except in the presence of very thin triangles. I suspect that derivative estimation at the vertices has problems on the edges and may very well be influenced by the convexity.

linear on a fine grid will probably look pretty good for you.

4. to get something as nice as the mayavi sample, you will probably need a fine rectangular mesh (maybe 200x200).

I tested the tinterp program in octave for a number of problems and found that the quadratic option gave nice results when I did not have functional discontinuities, and when I had good triangulations. I have been meaning to translate this to Python, so thanks for the motivation.

At the very least, this program may help you appreciate John's suggestions more.

Cheers,
Eric

Ondrej Certik wrote:

tinterp.py (10.2 KB)

···

Ok, I made a progress, it seems it's working. Script and picture

Forgot to attach the script.

Ondrej

------------------------------------------------------------------------

------------------------------------------------------------------------------
Register Now for Creativity and Technology (CaT), June 3rd, NYC. CaT
is a gathering of tech-side developers & brand creativity professionals. Meet
the minds behind Google Creative Lab, Visual Complexity, Processing, & iPhoneDevCamp asthey present alongside digital heavyweights like Barbarian
Group, R/GA, & Big Spaceship. http://www.creativitycat.com

------------------------------------------------------------------------

_______________________________________________
Matplotlib-users mailing list
Matplotlib-users@lists.sourceforge.net
matplotlib-users List Signup and Options

8

delaunay has a linear interpolator implemented in C++ that could be used for this purpose, too. The natural neighbor interpolator is only for Delaunay triangulations, but the linear interpolator should be usable for general triangulations.

···

On 2009-05-23 17:17, Eric Carlson wrote:

I should read entire posts before sending people down the wrong
pathways. I just happened to be working on a Python equivalent to MATLAB
"triplot" stuff when I read your subject line and made the wrong
assumptions. That program does just plot the edges, as you noted.

I have attached a python program, much of which is a translation of a
program I found at M*B central, contributed from the outside. Given a
triangulation, it allows you to interpolate on a regular rectangular
grid (dx=constant, dy=another constant). In your case, it should allow
you to use your original triangulation, and should avoid the convex hull
artifacts of your original griddata plot. I do not know if this new
program will give you a figure that will look as good as your latest
based on John's suggestion or not.

--
Robert Kern

"I have come to believe that the whole world is an enigma, a harmless enigma
  that is made terrible by our own mad attempt to interpret it as though it had
  an underlying truth."
   -- Umberto Eco

9

Hello Robert,
I studied delaunay and mlab.griddata a bit while converting tinterp and saw the

"""
         tri = delaunay.Triangulation(x,y)
         # interpolate data
         interp = tri.nn_interpolator(z)
         zo = interp(xi,yi)
"""
stuff. In studying delaunay, however, it was/is not clear to me how to set up the "triangulation" for

delaunay.LinearInterpolator(triangulation, z, default_value=-1.#IND)

without going through delaunay. Any chance you could give an example of using delaunay to linearly interpolate on mesh x,y assuming data_pts, triangles, f_at_data_points are already given?

Best Regards,
Eric

Robert Kern wrote:

···

delaunay has a linear interpolator implemented in C++ that could be used for this purpose, too. The natural neighbor interpolator is only for Delaunay triangulations, but the linear interpolator should be usable for general triangulations.

10

Ondrej Certik wrote:

Thanks a lot John. I tried that and it does what I want. I just need
to convert and probably average my 3 different values at the 3
vertices of the triangle and color the triangle with that color. When
I get it working, I'll send you a picture. :slight_smile:

Ok, I made a progress, it seems it's working. Script and picture
attached. You can compare to the mayavi plot above, it's almost
identical now. It took my some time playing with different parameters
of mpl to get here and I think it looks quite good. Still one can see
the artefacts though as John predicted, due to mpl not interpolating
the triangles.

Nice!

Just to prod you a bit: If you want to get rid of the hard mayavi dependence of femhub for 3D plots too, you could hack a (perspective/whatever) projection of 3D surface to 2D, remove invisible faces (normal points backwards) and plot the rest by the painter's algorithm (far faces first).

r.

···

On Fri, May 22, 2009 at 3:37 PM, Ondrej Certik <ondrej@...2033...> wrote:

11

Well, I spent one afternoon playing with cairo, trying to implement
the triangle interpolation and the result was slower than matplotlib.
So gave up and I'll just use what can be done with mpl currently.

As to mayavi, I'd rather make it easier to install. The only tough
dependency is VTK, that takes lots of time to build, we already got
rid of all the others, so that's good.

Ondrej

···

On Mon, May 25, 2009 at 1:03 AM, Robert Cimrman <cimrman3@...1098...> wrote:

Ondrej Certik wrote:

On Fri, May 22, 2009 at 3:37 PM, Ondrej Certik <ondrej@...2033...> wrote:

Thanks a lot John. I tried that and it does what I want. I just need
to convert and probably average my 3 different values at the 3
vertices of the triangle and color the triangle with that color. When
I get it working, I'll send you a picture. :slight_smile:

Ok, I made a progress, it seems it's working. Script and picture
attached. You can compare to the mayavi plot above, it's almost
identical now. It took my some time playing with different parameters
of mpl to get here and I think it looks quite good. Still one can see
the artefacts though as John predicted, due to mpl not interpolating
the triangles.

Nice!

Just to prod you a bit: If you want to get rid of the hard mayavi dependence
of femhub for 3D plots too, you could hack a (perspective/whatever)
projection of 3D surface to 2D, remove invisible faces (normal points
backwards) and plot the rest by the painter's algorithm (far faces first).

12

Hmm, true. I violated my own principle of trying not to do too much in the constructor. However, you should be able to figure out how to use the underlying utility functions compute_planes() and linear_interpolate_grid() from the LinearInterpolator code and Triangulation's docstring to describe its attributes.

···

On 2009-05-23 21:35, Eric Carlson wrote:

Hello Robert,
I studied delaunay and mlab.griddata a bit while converting tinterp and
saw the

"""
          tri = delaunay.Triangulation(x,y)
          # interpolate data
          interp = tri.nn_interpolator(z)
          zo = interp(xi,yi)
"""
stuff. In studying delaunay, however, it was/is not clear to me how to
set up the "triangulation" for

delaunay.LinearInterpolator(triangulation, z, default_value=-1.#IND)

without going through delaunay. Any chance you could give an example of
using delaunay to linearly interpolate on mesh x,y assuming data_pts,
triangles, f_at_data_points are already given?

--
Robert Kern

"I have come to believe that the whole world is an enigma, a harmless enigma
  that is made terrible by our own mad attempt to interpret it as though it had
  an underlying truth."
   -- Umberto Eco