Issues Plotting Projection of Hemisphere

Community
1

I have a grid of longitudes and latitudes of a visible hemisphere as well as a function of those longitudes and latitudes. I would like to plot a “disco ball” with the color of each facet/grid point representing the value of the function. The grid is initialized like so:

longs = np.linspace(-np.pi, np.pi, 15)
lats = np.linspace(-np.pi, np.pi, 15)

u, v = np.meshgrid(longs, lats)

and the function is something like:

func = N * np.sin(u) * np.cos(v).

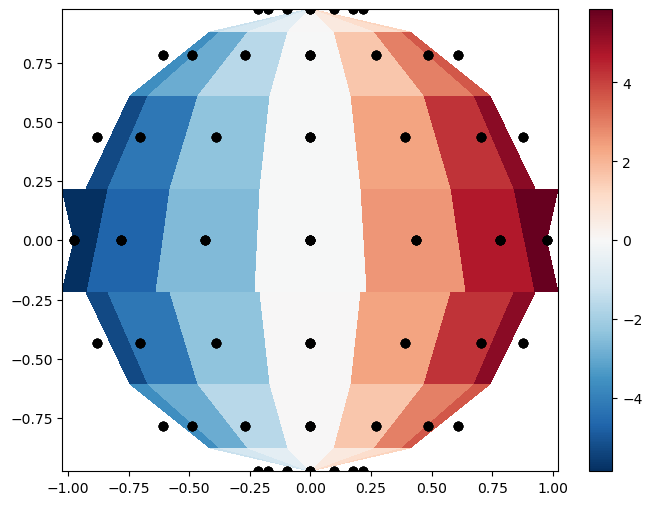
At first, I tried to project these onto (x,y) coordinates and plot with pcolormesh, however the cells are not centered on my grid points. The following code yields the below plot:

plt.figure(figsize=(8,6))
#plot the grid points
plt.plot(x, y, ‘ko’)
#colormesh
plt.pcolormesh(x, y, func, cmap=‘RdBu_r’)
plt.colorbar()
plt.show()

image
image652×505 19.7 KB

As can be seen, near the edges, the cells aren’t centered on the black grid points, and there is an odd behavior near the equator.

I then tried converting to polar coordinates to see if that would help. In terms of cell location, things are better, but there is still some odd behavior as shown in the picture:

phi = np.arctan2(y,x)
Rs = np.sqrt(x2 + y2)
theta = np.arcsin(Rs)

fig = plt.figure()
fig.add_axes([0.1,0.1,0.8,0.8],polar=True)
plt.pcolormesh(phi, Rs , func, shading=‘nearest’, cmap=‘RdBu_r’)
plt.colorbar()
plt.show()

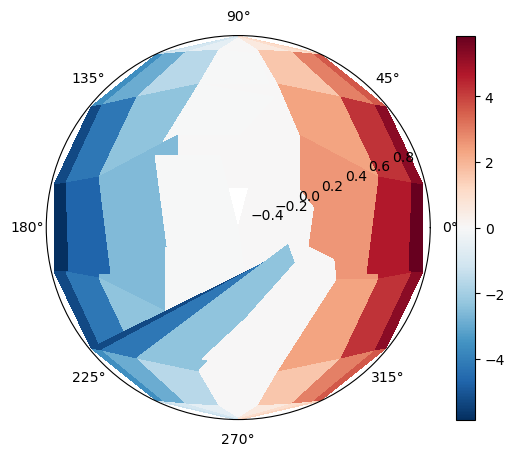
download

How can I fix these behaviors and/or is there a better way for me to create this visualization?

2

I discovered a bug and this has been mostly resolved

1 Like
3

This is a response regarding ‘a better way … to create this visualization’ for a ‘disco ball’. Maybe a 3D visualization would be appropriate. For example:

resp_1

where the code is

import numpy as np
import matplotlib.pyplot as plt
import s3dlib.surface as s3d

# 1. Define function to examine ...........................
def func(rtp) :
    r,t,p = rtp
    return np.sin(p)*np.cos(t)

# 2. Setup and map surfaces ...............................
surface = s3d.SphericalSurface.grid(7,15,'r')
surface.transform(s3d.eulerRot(-6,0))  # shift face centers
surface.map_cmap_from_op(func,'RdBu_r')

# 3. Construct figure, add surface, plot ..................
fig = plt.figure(figsize=plt.figaspect(1))
ax = plt.axes(projection='3d')
ax.set(xlim=(-1,1), ylim=(-1,1), zlim=(-1,1))

ax.add_collection3d(surface.shade(.5)) # w/ shading

fig.tight_layout(pad=1)
plt.show()

The 3D disco ball could be viewed as 2D by setting the axes’ elevation to 90 using view_init. For example see https://s3dlib.org/examples/datagridmap/mri_3d.html.