Hi folks!
I’m looking for some help developing napari. We’re having an issue with displaying polygons with holes in them, which matplotlib handles just fine. I tried to step through the matplotlib code for drawing a filled polygon but got lost rather quickly. 
I’m hoping someone here can point me to the algorithm that matplotlib uses to draw these, so we can reuse it in napari.
Polygons with holes seem to commonly be represented in map data as a single polygon with a back-and-forth edge from the external contour to the internal contour, where the internal contour uses the opposite winding direction to the outer contour. You can find the polygon from the full example in this gist, but everything works with a toy example so I’ll use that below.
Here’s a minimum reproducible example:
import matplotlib.pyplot as plt
import numpy as np
embedded = np.array(
[[ 0, 0], # outer triangle 0
[ 0, 100], # outer triangle 1 (clockwise)
[100, 50], # outer triangle 2
[ 50, 30], # go to inner triangle 0
[ 50, 70], # inner triangle 1
[ 20, 50], # inner triangle 2 (counterclockwise)
[ 50, 30], # back to inner triangle 0
[100, 50]] # back to outer triangle 2
) # final edge to outer triangle 0 implicit
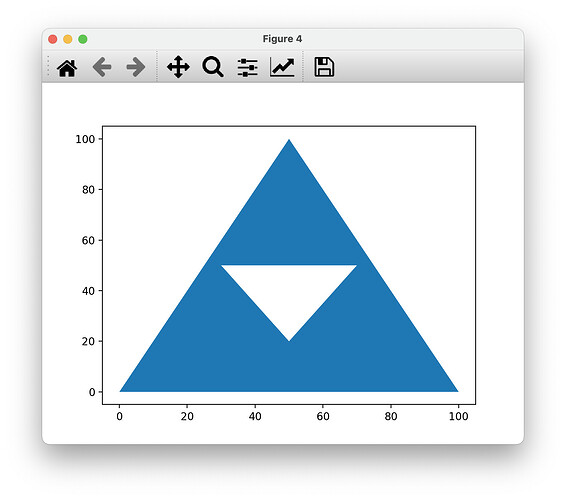
fig, ax = plt.subplots()
ax.fill(embedded[:, 1], embedded[:, 0])
plt.show()
This results in:
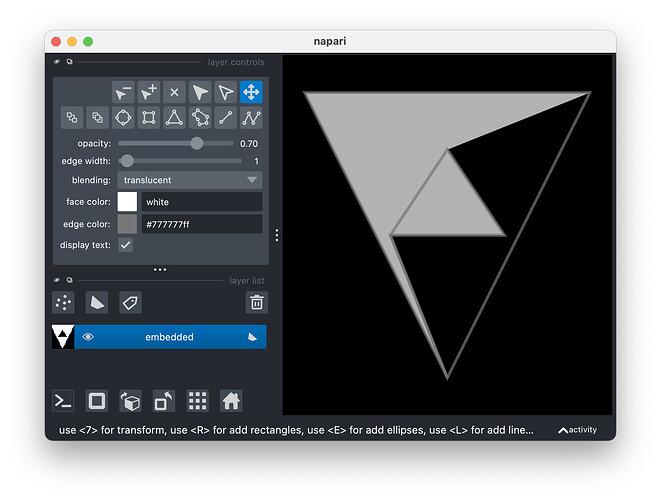
Compare that with napari’s output (you can install napari with pip install napari[pyqt]):
import napari
viewer = napari.Viewer()
viewer.add_shapes(embedded, shape_type='polygon')
napari.run() # not needed in IPython
As you can see we have some catching up to do…
On the napari side, what we are doing is passing the data to VisPy’s PolygonData(), using its triangulate() method (actually implemented here), then adding those triangles to a mesh.
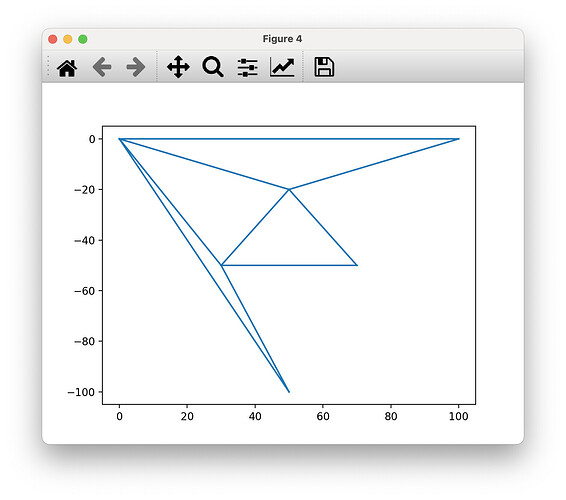
Thanks to Matplotlib’s triangulation plots, it’s easy to see how it’s going wrong:
from vispy.geometry.polygon import PolygonData
vertices, triangles = PolygonData(vertices=embedded).triangulate()
fig, ax = plt.subplots()
# note: I invert y to match napari which uses row/column coordinates
ax.triplot(vertices[:, 1], -vertices[:, 0], triangles)
So, my questions:
- is there code deep in Matplotlib’s bowels that would give me the correct triangulation of my polygon-with-a-hole?
- if so, where?
- if not, how is matplotlib actually drawing this data?
- also if not, can people point me to strategies, and ideally implementations, for the correct triangulation of such polygon data? My current naive/brute-force idea:
- get the Delaunay triangulation of the points using
scipy.spatial.Delaunay(which includes triangles both inside and outside of the polygon, see below) - find the center of each triangle
- use
skimage.measure.points_in_polyto determine whether it is inside the polygon - keep and draw only those triangles for which the center is in the polygon
- get the Delaunay triangulation of the points using
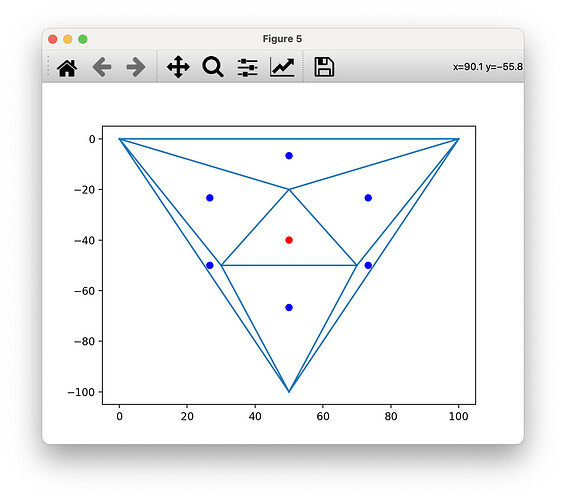
Here’s the Delaunay triangulation from that polygon data, with centers colored by points_in_poly:
from scipy.spatial import Delaunay
from skimage.measure import points_in_poly
delaunay = Delaunay(embedded)
centers = np.mean(embedded[delaunay.simplices], axis=1)
in_poly = points_in_poly(centers, embedded)
fig, ax = plt.subplots()
ax.triplot(embedded[:, 1], -embedded[:, 0], delaunay.simplices)
ax.scatter(
centers[:, 1], -centers[:, 0],
color=np.where(in_poly, 'blue', 'red'),
)
plt.show()
Is there a faster/more efficient way to do this or is this basically The Way?
Thanks for any insights you can provide! 
That took me to some old papers which unfortunately are not the type of classic that gives you an elegant, easy-to-implement algorithm in pseudocode. 