Generating N regularly spaced points on a sphere

Community matplotlib-users
1

Is there a method built into Numpy/SciPy or friends that will generate
a set of N points evenly (regularly - not randomly) sampling the
entire surface of a sphere? I imagine people doing GCMs and other
geoscience in spherical coordinates have to do this pretty frequently,
so I'm sure someone's written it in Python somewhere. My searches
aren't turning anything up immediately though.

Thanks,
Zane

···

--
Zane A. Selvans
Amateur Earthling
http://zaneselvans.org
+1 303 815 6866

2

Zane Selvans wrote:

Is there a method built into Numpy/SciPy or friends that will generate
a set of N points evenly (regularly - not randomly) sampling the
entire surface of a sphere? I imagine people doing GCMs and other
geoscience in spherical coordinates have to do this pretty frequently,
so I'm sure someone's written it in Python somewhere. My searches
aren't turning anything up immediately though.

Thanks,
Zane

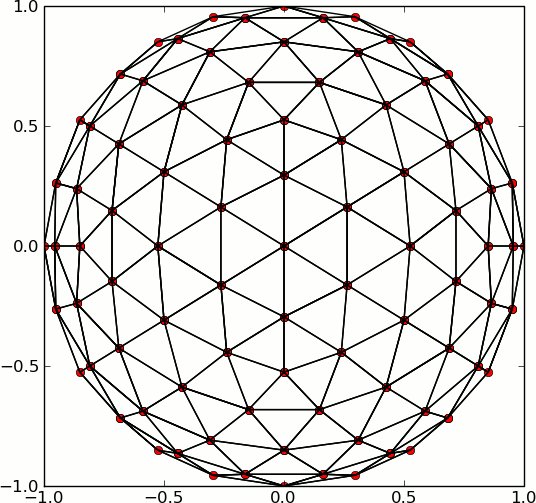
Zane: This one has puzzled mathematicians for centuries - there is no evenly spaced set of points on a sphere. The golden section spiral (or fibonacci) points are easy to code (see code below), but don't form the vertices of polygons. For modelling, where you need the points to be vertices of polygons, hexagonal icosahedral grid are typically used (see http://kiwi.atmos.colostate.edu/BUGS/geodesic/), but they are tricky to compute (I don't have any python code handy).

Regards,

-Jeff

import numpy as np
from mpl_toolkits.basemap import Basemap
import matplotlib.pyplot as plt
import sys

# from http://www.xsi-blog.com/archives/115

def fibonacci(N):
    inc = np.pi * (3 - np.sqrt(5))
    off = 2. / N
    r2d = 180./np.pi
    k = np.arange(0,N)
    y = k*off - 1. + 0.5*off
    r = np.sqrt(1 - y*y)
    phi = k * inc
    x = np.cos(phi)*r
    z = np.sin(phi)*r
    theta = np.arctan2(np.sqrt(x**2+y**2),z)
    phi = np.arctan2(y,x)
    lats = 90.-r2d*theta
    lons = r2d*phi
    return lats, lons

npts = int(sys.argv[1])

lats, lons = fibonacci(npts)

map = Basemap(projection ='ortho',lat_0=0,lon_0=-90)
map.drawcoastlines()
map.fillcontinents(color='coral')
map.drawmapboundary(fill_color='aqua')
x,y = map(lons, lats)
map.scatter(x,y,10,marker='o',zorder=10)
plt.show()

3

Jeff Whitaker wrote:

Zane Selvans wrote:

Is there a method built into Numpy/SciPy or friends that will generate
a set of N points evenly (regularly - not randomly) sampling the
entire surface of a sphere? I imagine people doing GCMs and other
geoscience in spherical coordinates have to do this pretty frequently,
so I'm sure someone's written it in Python somewhere. My searches
aren't turning anything up immediately though.

Thanks,
Zane

Zane: This one has puzzled mathematicians for centuries - there is no
evenly spaced set of points on a sphere. The golden section spiral (or
fibonacci) points are easy to code (see code below), but don't form the
vertices of polygons. For modelling, where you need the points to be
vertices of polygons, hexagonal icosahedral grid are typically used (see
http://kiwi.atmos.colostate.edu/BUGS/geodesic/), but they are tricky to
compute (I don't have any python code handy).

I'm attaching some code I wrote to subdivide and icosahedron for tiling
a sphere with hexagons (and the occasional pentagon).

-Andrew

subdivided_icosahedron.png
subdivided_icosahedron.png536×503 40.9 KB

subdivided_icosahedron.py (3.05 KB)