Drawing segments (tangents) of fixed lengths preserving the aspect angles with matplotlib

[u_x]

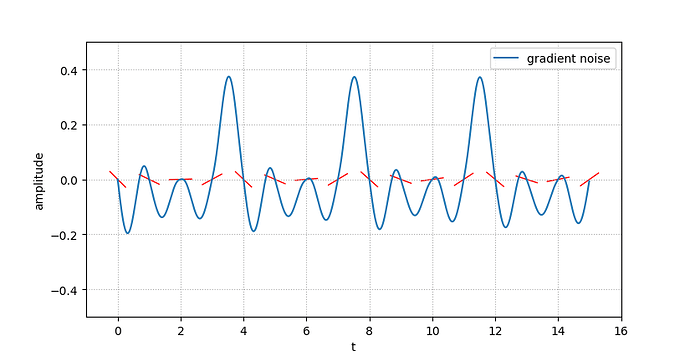
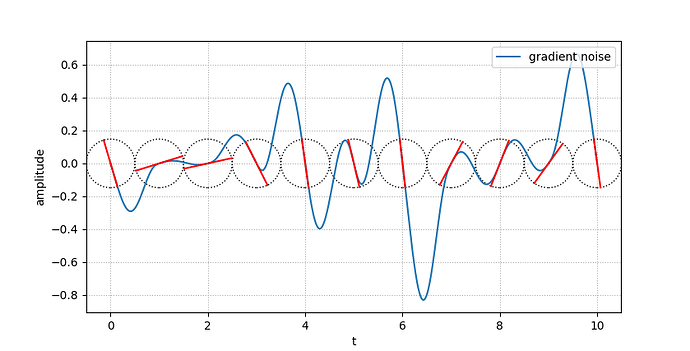
Context: I’m trying to display the gradients as fixed-length lines on a plot of gradient noise. Each “gradient” can be seen as a tangent on a given point. The issue is, even if I make sure the lines have the same length, the aspect ratio stretches them:

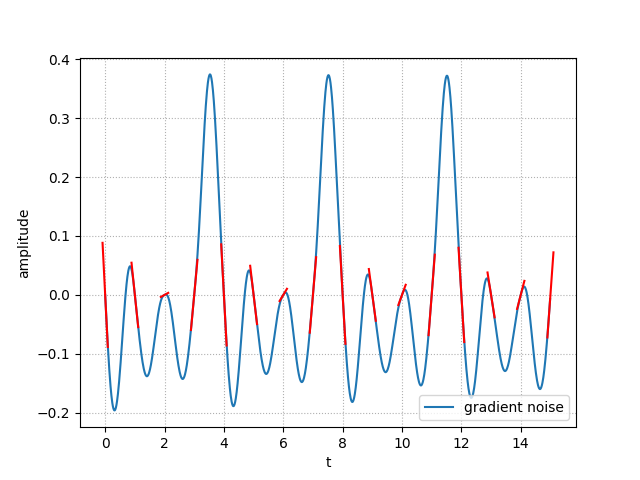
The complete code to generate this:

from math import sqrt, floor
import matplotlib.pyplot as plt

mix = lambda a, b, x: a*(1-x) + b*x
interpolant = lambda t: ((6*t - 15)*t + 10)*t*t*t
rng01 = lambda x: ((1103515245*x + 12345) % 2**32) / 2**32

def _gradient_noise(t):
    i = floor(t)
    f = t - i
    s0 = rng01(i)     * 2 - 1
    s1 = rng01(i + 1) * 2 - 1
    v0 = s0 * f;
    v1 = s1 * (f - 1);
    return mix(v0, v1, interpolant(f))

def _plot_noise(n, interp_npoints=100):
    xdata = [i/interp_npoints for i in range(n * interp_npoints)]
    gnoise = [_gradient_noise(x) for x in xdata]

    plt.plot(xdata, gnoise, label='gradient noise')
    plt.xlabel('t')
    plt.ylabel('amplitude')
    plt.grid(linestyle=':')
    plt.legend()

    for i in range(n + 1):
        a = rng01(i) * 2 - 1  # gradient slope
        norm = sqrt(1 + a**2)
        norm *= 4  # 1/4 length
        vnx, vny = 1/norm, a/norm
        x = (i-vnx/2, i+vnx/2)
        y = (-vny/2, vny/2)
        plt.plot(x, y, 'r-')

    plt.show()

if __name__ == '__main__':
    _plot_noise(15)

The red-lines drawing is located in the for-loop.

hypot(x[1]-x[0], y[1]-y[0]) gives me a constant .25 for every vector, which corresponds to my target length (¼). Which means my segments are actually in the correct length for the given aspect. This can also be “verified” with .set_aspect(1).

I’ve tried several things, such as translating the coordinates into display coordinates (plt.gca().transData.transform(...)), scale them, then back again (plt.gca().transData.inverted().transform(...)), without success (as if the aspect was applied on top of the display coordinates). Doing that would probably also actually change the angles as well anyway.

So to sum up: I’m looking for a way to display lines with a fixed length (expressed in the x data coordinates system), and oriented (rotated) in the xy data coordinates system.

[u_x]

One direction I investigated was to try to display a round circle:

• in a non-orthogonal coordinates system
• at a position expressed in that coordinate system
• and its radius expressed in the unit of the x-axis

I tried building an ellipse, using the aspect ratio, but still can’t manage to get it right.

[jklymak]

I mean if the line is the same length but at different angles, but the aspect ratio is stretched then the lines will be stretched… Why is that a problem?

[u_x]

They’re tangents so I want them to honor the coordinates system for their angle, but at the same time I want to keep their length the same visually.

[jklymak]

I think if a is the aspect ratio, you multiply by both your dx and dy by b = np.sqrt(1/(dx**2 + a**2 *dy**2))

[QuLogic]

As a completely different idea, mplsoccer has a scatter method that accepts rotation angle per scatter point:
https://mplsoccer.readthedocs.io/en/latest/gallery/plots/plot_rotated_markers.html
You could do scatter use vline or hline markers, rotated by the angle of the slope.

I don’t know if it’s directly translatable to plain Matplotlib, but there might be some inspiration in there.

[u_x]

@jklymak

I think if a is the aspect ratio, you multiply by both your dx and dy by b = np.sqrt(1/(dx**2 + a**2 *dy**2))

I don’t understand your suggestion: if I multiply both the x and y coordinates by a constant they will be scaled proportionally, but in the data coordinate space they need to be morphed.

[u_x]

@QuLogic

As a completely different idea, mplsoccer has a scatter method that accepts rotation angle per scatter point:
https://mplsoccer.readthedocs.io/en/latest/gallery/plots/plot_rotated_markers.html
You could do scatter use vline or hline markers, rotated by the angle of the slope.

I don’t know if it’s directly translatable to plain Matplotlib, but there might be some inspiration in there.

Yeah I’ve been trying to use annotations/markers but kinda failed in various ways every time. What I try to achieve seems actually really tricky, I wonder why.

I will into mplsoccer though, thanks.

[jklymak]

You want each line to be longer or shorter so that they are all visually the same length, but preserve the visual angle of the line. You need to multiply dx and dy by the same factor, or the visual angle will change. b is that factor, though it may be 1 / (aspect**2 *dx**2 + dy**2), but you can easily figure that out.

Perhaps I confused you by using a, which you are using for something else…

[u_x]

So I tried this scatter/rotate approach used in mplsoccer, and unfortunately as I though the rotate doesn’t happen in the appropriate space:

    x = list(range(n + 1))
    y = [0] * len(x)
    angles = [atan(rng01(i) * 2 - 1) for i in x]

    sc = ax.scatter(x, y, c='r', s=400)
    paths = []
    for angle in angles:
        m = mmarkers.MarkerStyle('_')
        trf = m.get_transform().rotate(angle)
        paths.append(m.get_path().transformed(trf))
    sc.set_paths(paths)

As you can see, the angles are incorrect.

[u_x]

@jklymak

You want each line to be longer or shorter so that they are all visually the same length, but preserve the visual angle of the line. You need to multiply dx and dy by the same factor, or the visual angle will change. b is that factor, though it may be 1 / (aspect**2 *dx**2 + dy**2), but you can easily figure that out.

Ah yeah sorry my bad; yeah the thing is I think I have the aspect ratio wrong, because I did try something like that a while. Here is how I compute the aspect ratio:

import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse


ax = plt.gca()
ax.set_xlim(0, 16)
ax.set_ylim(-.5, .5)
xlim = ax.get_xlim()
ylim = ax.get_ylim()
ar = (xlim[1] - xlim[0]) / (ylim[1] - ylim[0])
w = 3
ax.add_patch(Ellipse(xy=(8, 0), width=w, height=w/ar))
plt.show()

Which gives me:

…which is obviously not round.

[jklymak]

You want ar = ax.get_aspect() (ahem or ar = 1 / ax.get_aspect(), I always forget)

[u_x]

ax.get_aspect() is a string set to "auto"

[jklymak]

Ha ha, thats useless. I guess someone should add a kwarg to return the actual aspect ratio:

I think it is:

fs = ax.figure.get_size_inches()
pos = ax.get_position(original=False)
ar = 1/(fs[0] *pos.width /fs[1] / pos.height * ax.get_data_ratio())

[u_x]

This is still not round… and actually depends on the size of the window (If I resize, it breaks)

[jklymak]

It certainly works for me, but yes, if you resize you need to recalculate because the aspect ratio changes. Unfortunately there is no transform that does what you want: angle in data space, but size in physical space. You can certainly add a resize callback that recalculates the x and y data of the line if needed.

[u_x]

@jklymak

It certainly works for me

My bad: my windows manager was resizing right away so I never got the correct size (but it was indeed working just fine with an export).

@jklymak

You can certainly add a resize callback that recalculates the x and y data of the line if needed.

Alright, I just did that and it seems to finally work as I expected:

import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse


def _get_ar(ax):
    fs = ax.figure.get_size_inches()
    pos = ax.get_position(original=False)
    return 1 / (ax.get_data_ratio() * (fs[0] * pos.width) / (fs[1] * pos.height))


def _main():
    ax = plt.gca()
    ax.set_xlim(0, 16)
    ax.set_ylim(-.5, .5)
    ar = _get_ar(ax)

    ellipse_d = 4
    ellipse = Ellipse(xy=(8, 0), width=ellipse_d, height=ellipse_d / ar)

    def _onresize(event):
        ellipse.height = ellipse_d / _get_ar(ax)

    ax.add_patch(ellipse)
    ax.figure.canvas.mpl_connect('resize_event', _onresize)

    plt.show()


if __name__ == '__main__':
    _main()

I must say, such complexity is far beyond what I’d expect…

Thanks a lot.

[u_x]

For the record, here is the finale plot and code:

import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse

from math import hypot, floor, modf, sin

mix = lambda a, b, x: a*(1-x) + b*x
interpolant = lambda t: ((6*t - 15)*t + 10)*t*t*t
rng01 = lambda x: modf(sin(x) * 43758.5453123)[0]


def _gradient_noise(t):
    i = floor(t)
    f = t - i
    s0 = rng01(i)     * 2 - 1
    s1 = rng01(i + 1) * 2 - 1
    v0 = s0 * f;
    v1 = s1 * (f - 1);
    return mix(v0, v1, interpolant(f))


def _get_ar(ax):
    fs = ax.figure.get_size_inches()
    pos = ax.get_position(original=False)
    return 1 / (ax.get_data_ratio() * (fs[0] * pos.width) / (fs[1] * pos.height))


def _get_line_coords(aspect, i):
    dx, dy = 1, rng01(i) * 2 - 1  # gradient slope
    norm = hypot(dx, dy * aspect)
    vnx, vny = dx/norm, dy/norm
    x = (i-vnx/2, i+vnx/2)
    y = (-vny/2, vny/2)
    return x, y


def _plot_noise(n, interp_npoints=100):
    xdata = [i/interp_npoints for i in range(n * interp_npoints)]
    gnoise = [_gradient_noise(x) for x in xdata]

    fig, ax = plt.subplots()
    ax.plot(xdata, gnoise, label='gradient noise')
    ax.set_xlabel('t')
    ax.set_ylabel('amplitude')
    ax.grid(linestyle=':')
    ax.legend(loc=1)

    xlim = ax.get_xlim()
    ylim = ax.get_ylim()

    aspect = _get_ar(ax)
    resize_objects = []
    for i in range(n + 1):
        lx, ly = _get_line_coords(aspect, i)
        line = ax.plot(lx, ly, 'r-')[0]
        ellipse = Ellipse(xy=(i, 0), width=1, height=1/aspect, fill=False, linestyle=':')
        ax.add_patch(ellipse)
        resize_objects.append((line, ellipse))

    def _onresize(event):
        ar = _get_ar(ax)
        for i, (line, ellipse) in enumerate(resize_objects):
            ellipse.set_height(1 / ar)
            lx, ly = _get_line_coords(ar, i)
            line.set_xdata(lx)
            line.set_ydata(ly)

    ax.figure.canvas.mpl_connect('resize_event', _onresize)

    ax.set_xlim(xlim)
    ax.set_ylim(ylim)

    plt.show()


if __name__ == '__main__':
    _plot_noise(10)