Coherence in matplotlib and/or scipy.signal

[machielk]

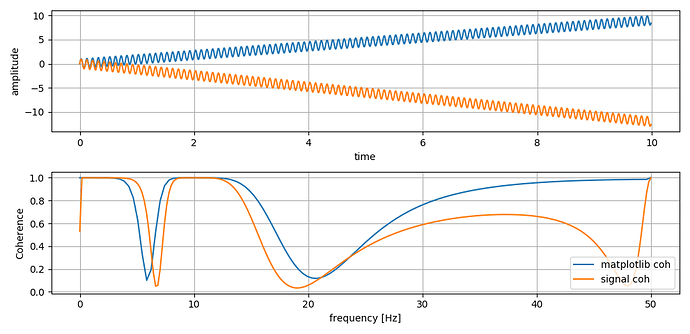
I have a - naive - code to calculate the coherence between two signals.

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
 
# Create sine wave1
timestep = 0.01
time        = np.arange(0, 10, timestep)
freq = 10 # Hz
sinewave1   = np.sin(2.0 * np.pi * freq * time)
sinewave1  += 0.9*time;

# Create sine wave2 
sinewave2   = np.sin(2.0 * np.pi * freq * time)
sinewave2  += -1.2*time;

# Plot the sine waves 
plt.subplot(211)
plt.grid(True, which='both')
plt.xlabel('time')
plt.ylabel('amplitude')
plt.plot(time, sinewave1, time, sinewave2)

# Plot the coherences 
plt.subplot(212)
coh, f = plt.cohere(sinewave1, sinewave2, 256, 1./timestep, label="matplotlib coh")
plt.xlabel('frequency [Hz]')
plt.ylabel('coherence')

f, Cxy = signal.coherence(sinewave1, sinewave2, 1./timestep, nperseg=512)
plt.plot(f, Cxy, label="signal coh")
plt.legend(loc="lower right")
plt.show()

I would expect a peak at 10Hz in the coherence plots but instead I get these strange curves. Could anyone tell me what I am doing wrong or forward me to information that could instruct me?

[jklymak]

These are highly coherent at all frequencies, so I don’t think these results are surprising. Add uncorrelated noise to each signal to see a peat at 10 Hz…

[machielk]

Hi,

Thank you for your fast reply. I added the following:

rng = np.random.default_rng()
noise_power = 12.0
noise1 = rng.normal(scale=np.sqrt(noise_power), size=time.shape)
sinewave1 += noise1
noise2 = rng.normal(scale=np.sqrt(noise_power), size=time.shape)
sinewave2 += noise2

And this makes the signals noisier but I still don’t see the peak at 10 Hz.