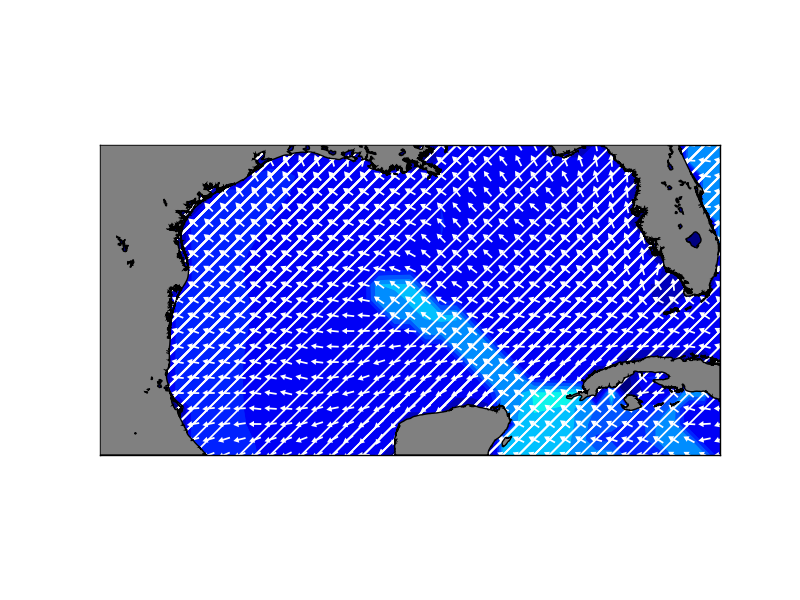
Hi,
I just updated to the latest versions of mpl & basemap.
Im getting strange output when using the quiver function from basemap (see
attached image).
I ran the quiver_demo scripts for both basemap & also mpl, and the output
looked normal.
Im using pygrads, a python interface to GrADS, in order to generate my
X,Y,U,V input arrays for quiver.
I can provide these arrays if needed...
The data imported using pygrads previously worked fine (prior to updating to
the new versions).
Before I start diving into the pygrads code in order to troubleshoot, I
wanted to first check to see if this issue is a possible quiver bug in the
new version(s)...
Or, were there any significant changes to the mpl/basemap code with respect
to how quiver works???
Here's the basic method Im using...
U = <my_pygrads_imported_U>
V = <my_pygrads_imported_V>
X,Y=m(*np.meshgrid(U.grid.lon,U.grid.lat))
#x,y,u,v = delete_masked_points(X.ravel(), Y.ravel(), U.ravel(), V.ravel())
cs2 = m.quiver(X,Y,U,V,*kwargs)
again, this *used* to work fine, prior to the updates...
Please help,
Thanks,
P.Romero