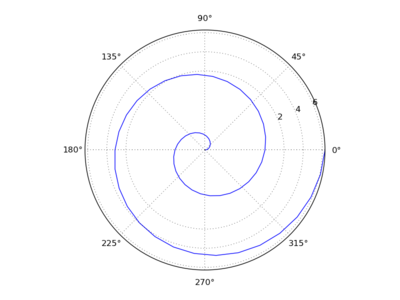
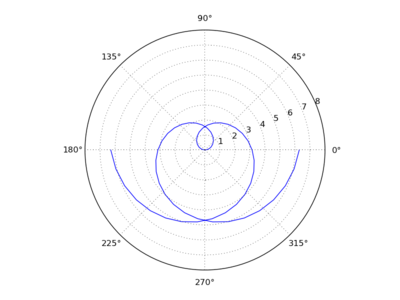
Hi Brendan,
I reiterate that in polar coordinates, a negative value of "r"
does not make sense. It is confusing at best.
This isn't really true. Many standard introductions to polar
coordinates consider negative r as valid. It's simply treated as
a radius in the opposite direction
In Euclidean space, can you have a negative distance? Would you
ever describe a circle as having negative radius (in Euclidean
space)? If you take "r" to be the radius, then I suggest you
confuse a precise definition of radius with allowing a useful,
non-unique interpretation of negative values of "r".
I don't take r to be "the radius", I take it to be a number in an ordered pair with a particular mapping into R^2. It is an extension of the notion of radius, but there's no reason it has to conform with the restrictions on geometrically possible radii.
This was clear from your previous comment - but this is precisely my point. In your original message, you used the word "radius". My point is that mathematics, and computing, are precise languages with hopefully unambiguous definitions. You used the word radius, but had in mind a less rigorous definition, because you were thinking of "r" as just one component of a two-coordinate description of 2D Euclidean space, with a specific definition of how to interpret negative "r". It is the standard you are used to and so not surprising to you. My point is that this expectation is not unique, and in my field, not common, and so not expected by me. Further, looking at the matplotlib doc, there is no indication what is happening - from
http://matplotlib.org/api/pyplot_api.html
matplotlib.pyplot.polar(*args, **kwargs)
Make a polar plot.
call signature:
polar(theta, r, **kwargs)
Multiple theta, r arguments are supported, with format strings, as in plot().
There is no mention in the docs about the treatment of negative "r". The treatment is contrary to my expectations, and I would wager contrary to many peoples expectations. So at a new minimum, at the very least, the docs should make clear what is happening.
I would further suggest that there are options specified by kwargs what the behavior is. The default could be the current behavior, which sounds like it is standard to some, and another option would be to complain if r < 0, as I think many others would expect.
Maybe I am totally off. Maybe I am the only one who does not expect r to go negative. But at least the behavior should be clear without having to dig into the code.
However, those issues are beside the point. The point is that, regardless of what a radius is, in the context of polar coordinates, a negative *r-coordinate* is a perfectly mathematically respectable notion with a standard interpretation. Moreover, it is actually useful when you want to graph some things, and is supported by other plotting software (see, e.g., polar plot r=theta,-pi<r<0 - Wolfram|Alpha). Matplotlib should plot r-coordinates according to this standard interpretation,
Again, I would just argue the standard behavior should be clearly stated in the docs.
Regards,
Andre