How to draw lines that are shaded/hashed to one side?

[md6211]

How can I draw lines that are shaded or hashed on one sides, the type of line that is used for boundaries on maps.

Here is an example:

[El_Uatu]

Welcome,

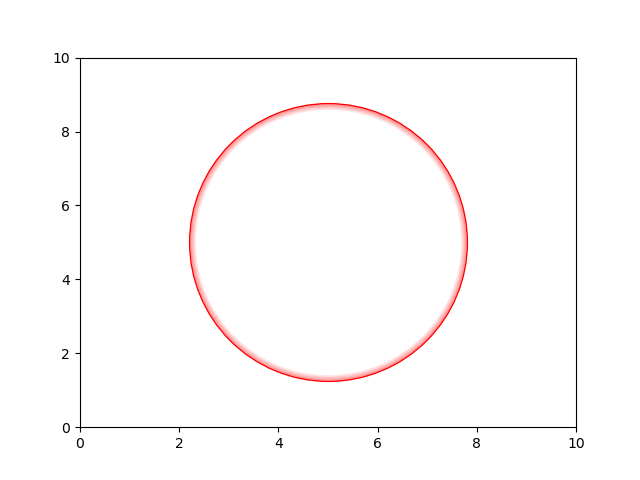
There are lot of ways, here is a blunt one :

import matplotlib.pyplot as plt

# Main plot
plt.plot( 5, 5, c ='None', marker = 'o', markersize = 200, markeredgecolor = 'red',
          markeredgewidth = 1, alpha=1)

# Shade - In a small loop decreases the size and the alpha

for m in range(1,6):
    plt.plot( 5, 5, c ='None', marker = 'o', markersize = 200-m*2, markeredgecolor = 'red',
              markeredgewidth = 1, alpha=0.5-m/10)

plt.ylim(0,10)
plt.xlim(0,10) 

plt.show()

Gives you :

[md6211]

Hi @El_Uatu, thank you very much for your suggestion!

I found a library that can calculate offset lines and switched to axis coordinates so that it works independent of the aspect ratio.
There are many corner cases, and the parallel_offset function might return a list of separate offsets, but for this simple case it looks very good.

import matplotlib.pyplot as plt
import numpy as np
from shapely.geometry import LineString

x=np.logspace(0,3,100)
y=x**2

fig, ax = plt.subplots()
p=ax.plot(x,y, color='k', linestyle='dashdot', linewidth=3)
pth = p[0].get_path()
# go to axes coordinates
X, Y = ax.transLimits.transform_path(pth).vertices.T

l=LineString(zip(X,Y))

for offset in np.linspace(0.2,1,10):
    # parallel_offset(distance, side, resolution=16, join_style=1, mitre_limit=5.0)
    # resolution = # of segments to approximate a quarter circle
    offsetScaling = 0.005
    l2=l.parallel_offset(offset*offsetScaling, side='right')
    x2, y2 = np.array(l2.coords).T
    # back to data coordinates
    xo, yo = ax.transLimits.inverted().transform(np.vstack((x2,y2)).T).T
    ax.plot(xo, yo, alpha=1-offset, color='red')

Thank you!

[El_Uatu]

You welcome !!!

Seems to be a useful lib you have found - did not know it at all - thanks for mentioning.

Rgds

[rob.a.mcdonald]

Version 3.4 will include this pull request which will produce plots like the attached.

Here are some of the examples for the dev version…

General use as a line style

Use in an optimization problem

[md6211]

Great! Exactly my application. Thanks!